Model Building
Models of the world are useful to decision makers. This is because they allow decision makers to better understand the system they must work with. They can explore behaviour in a model that is simply not practical to experiment with in real life. A model of the system can strip out the essence of a system from the mass of detail that confuse the picture in the real system. This clarity can lead to better and more informed decision making.
So, what is a model? Models can come in many forms. The kinds of problem structuring techniques described on the previous page of this website will produce models. These models may be descriptive models, but that does not stop them from being useful in understanding or representing the behaviour of the real world.
Explicit models of problems can bring surprising benefits, leading to joint understanding of problems by those who must work to solve them, miniature versions of reality in which new approaches can be trialled and a clearer grasp of driving parameters to allow the situation to be optimised and the best possible outcomes obtained.
So, what is a model? Models can come in many forms. The kinds of problem structuring techniques described on the previous page of this website will produce models. These models may be descriptive models, but that does not stop them from being useful in understanding or representing the behaviour of the real world.
Explicit models of problems can bring surprising benefits, leading to joint understanding of problems by those who must work to solve them, miniature versions of reality in which new approaches can be trialled and a clearer grasp of driving parameters to allow the situation to be optimised and the best possible outcomes obtained.
Descriptive Models
This kind of model is the sort that is produced by the problem-structuring techniques already discussed. The model does not necessarily have quantitative variables but provides a description of the system that can be shared by the various different people involved in dealing with that system.
The benefits of this should not be underestimated. The research on team learning clearly shows that one of the strongest indicators of team success is the existence of shared mental models. The kind of descriptive models that are generated by problem-structuring approaches can form the basis of this kind of shared mental model.
Descriptive models of this kind can be used as a basis for stimulating discussion on how to solve problems and can clarify aspects of the system that may be being given insufficient attention. Often decision-makers attention is focused upon one or two aspects of the system that require day-to-day attention, when the source of the problems may be in another area entirely. Descriptive models can capture broader views of the system, highlighting areas that are important but not necessarily prominent.
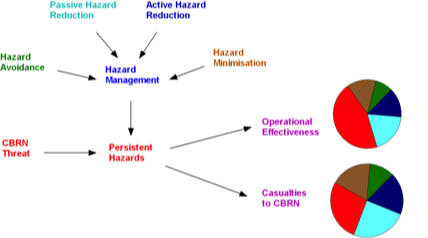
It is even possible to have different descriptive models of the same system at different levels of detail. The two examples shown to the right and below are models of the same system, but at different levels of detail. Both are purely descriptive in nature, and show relationships but are not quantitative.
The benefits of this should not be underestimated. The research on team learning clearly shows that one of the strongest indicators of team success is the existence of shared mental models. The kind of descriptive models that are generated by problem-structuring approaches can form the basis of this kind of shared mental model.
Descriptive models of this kind can be used as a basis for stimulating discussion on how to solve problems and can clarify aspects of the system that may be being given insufficient attention. Often decision-makers attention is focused upon one or two aspects of the system that require day-to-day attention, when the source of the problems may be in another area entirely. Descriptive models can capture broader views of the system, highlighting areas that are important but not necessarily prominent.
It is even possible to have different descriptive models of the same system at different levels of detail. The two examples shown to the right and below are models of the same system, but at different levels of detail. Both are purely descriptive in nature, and show relationships but are not quantitative.
Statistical Models
Statistical models are models that show important aspects of the behaviour of the system through exploration of statistical relationships. These models usually show correlation rather than causation, though in many real-world systems this can be a difficult distinction to make in any case.
Statistical models are quantitative and can give useful information for those needing to make practical day-to-day decisions. Many of the techniques referred to as analytics, or sometimes predictive analytics, are essentially statistical models of problems. They show how measures of effectiveness - such as sales for example - depend both upon factors within the power of the decision-maker (such as promotions and offers) and factors outside the power of the decision-maker (such as the day of the week or the weather).
Statistical models need to be used carefully. In complex, real-world systems the inter-connections between variables mean that effects that appear to be due to some obvious and important variable are in fact due to some third variable that is sometimes, but not always correlated with the obvious value. Despite this, statistical models of systems are widely used for credit-scoring, inventory control, decisions on opening new facilities and insurance pricing.
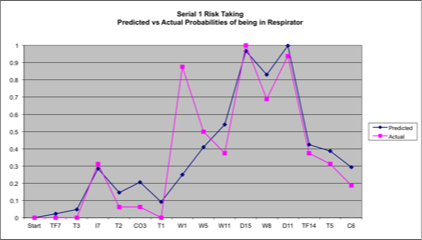
Statistical models can deal with complex and difficult problems such as human decision-making. The figures on the right are the results of applying models of human decision making to real data and show that when it is accepted that human decision making is probabilistic rather than deterministic substantial progress can be made on building useful models.
Statistical models are quantitative - unlike the descriptive models - but are static and silent on the critical issue of causation.
Statistical models are quantitative and can give useful information for those needing to make practical day-to-day decisions. Many of the techniques referred to as analytics, or sometimes predictive analytics, are essentially statistical models of problems. They show how measures of effectiveness - such as sales for example - depend both upon factors within the power of the decision-maker (such as promotions and offers) and factors outside the power of the decision-maker (such as the day of the week or the weather).
Statistical models need to be used carefully. In complex, real-world systems the inter-connections between variables mean that effects that appear to be due to some obvious and important variable are in fact due to some third variable that is sometimes, but not always correlated with the obvious value. Despite this, statistical models of systems are widely used for credit-scoring, inventory control, decisions on opening new facilities and insurance pricing.
Statistical models can deal with complex and difficult problems such as human decision-making. The figures on the right are the results of applying models of human decision making to real data and show that when it is accepted that human decision making is probabilistic rather than deterministic substantial progress can be made on building useful models.
Statistical models are quantitative - unlike the descriptive models - but are static and silent on the critical issue of causation.
System Models
System models take the key elements of descriptive models and simple statistical models and combine them to produce a quantitative model of the behaviour of the system that is based upon assessments of the effectiveness of the different components of the system, combined according to the role of the individual component within the system as a whole.
Thus for the simple system shown on the right, there are four components to the system, each of which is assumed to work independently and to be effective against a proportion of the overall threat. This gives a very simple measure of the effectiveness of the system, with its total effectiveness being calculated using the rules of probability.
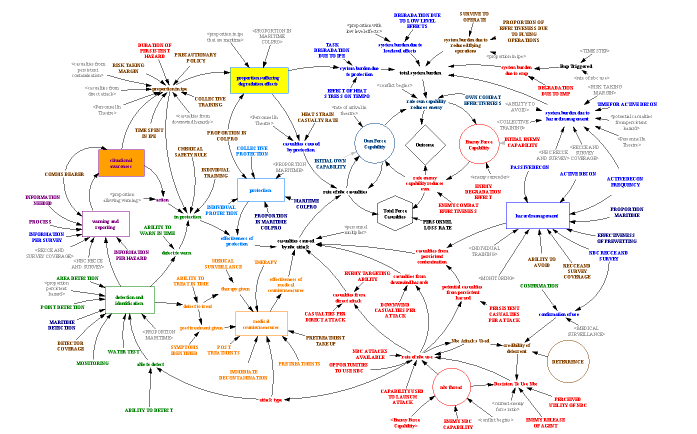
A much more complex example is shown below, where an entire defensive system is laid out. This model can carry out limited dynamic simulation but it is more of a tool for assessment of the system as a whole and a method of identifying where investments in capability are likely to give the greatest benefit.
Thus for the simple system shown on the right, there are four components to the system, each of which is assumed to work independently and to be effective against a proportion of the overall threat. This gives a very simple measure of the effectiveness of the system, with its total effectiveness being calculated using the rules of probability.
A much more complex example is shown below, where an entire defensive system is laid out. This model can carry out limited dynamic simulation but it is more of a tool for assessment of the system as a whole and a method of identifying where investments in capability are likely to give the greatest benefit.